고정 헤더 영역
상세 컨텐츠
본문
밀라 알고리즘 스터디 3주차 개념 정리
✍🏻DFS : 깊이 우선 탐색
: 최대한 깊이 내려간 뒤 , 더이상 깊이 갈 곳이 없을 경우 옆으로 이동
루트 노드에서 시작해서 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식
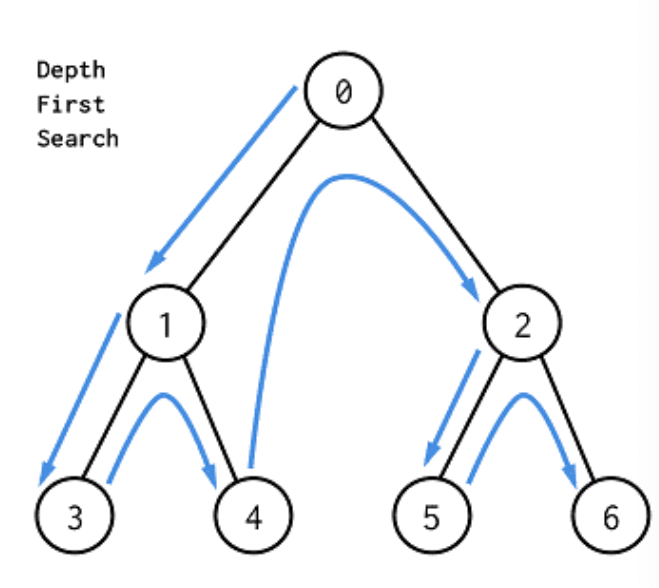
- 장점 : 코드가 직관적이고 구현이 쉬움
: 저장 공간의 필요성이 적음
- 단점 : 깊이가 엄청 깊어지면 메모리 비용이 지나치게 커질 수 있음
: 최단 경로를 알 수 없음
const graph = {
A: ['B', 'C'],
B: ['A', 'D'],
C: ['A', 'G', 'H', 'I'],
D: ['B', 'E', 'F'],
E: ['D'],
F: ['D'],
G: ['C'],
H: ['C'],
I: ['C', 'J'],
J: ['I']
};
const DFS = (graph, startNode) => {
const visited = [];
let needVisit = [];
needVisit.push(startNode);
while (needVisit.length !== 0) {
const node = needVisit.shift();
if (!visited.includes(node)) {
visited.push(node);
needVisit = [...graph[node], ...needVisit];
}
}
return visited;
};
✍🏻BFS : 너비 우선 탐색
: 최대한 넓게 이동한 다음 , 더 이상 갈 수 없을 때 아래로 이동
루트노드에서 시작해서 인접한 노드를 먼저 탐색하는 방법
시작 정점으로부터 가까운 정점을 먼저 방문하고 멀리 떨어져 있는 정점을 나중에 방문하는 순회 방법

- 장점 : 너비를 우선으로 탐색하기 때문에 답이 되는 경로가 여러 개인 경우에도 최단 경로임을 보장
: 노드의 수가 적고 싶이가 얕을 때 유리함
- 단점 : 구현이 비교적 까다로움
const graph = {
A: ['B', 'C'],
B: ['A', 'D'],
C: ['A', 'G', 'H', 'I'],
D: ['B', 'E', 'F'],
E: ['D'],
F: ['D'],
G: ['C'],
H: ['C'],
I: ['C', 'J'],
J: ['I']
};
const BFS = (graph, startNode) => {
let visited = [];
let needVisit = [];
needVisit.push(startNode);
while (needVisit.length !== 0) {
const node = needVisit.shift();
if (!visited.includes(node)) {
visited.push(node);
needVisit = [...needVisit, ...graph[node]];
}
}
return visited;
};
⏰시간복잡도
- 인접 리스트 : O(N+E)
- 인접 행렬 : O(N^2)
| DFS : Depth-First Search | BFS : Breadth-First Search |
| 현재 정점에서 갈 수 있는 점들까지 들어가며 탐색 | 현재 정점에서 연결된 가까운 점들부터 탐색 |
| 스택 또는 재귀함수로 구현 | 큐를 이용해서 구현 |
'밀라 알고리즘 스터디' 카테고리의 다른 글
| 백준 11724 : 연결 요소의 개수 (0) | 2025.01.21 |
|---|---|
| 백준 1260 : DFS와 BFS (0) | 2025.01.20 |
| 백준 14888 : 연산자 끼워넣기 (0) | 2025.01.18 |
| 백준 14889 : 스타트와 링크 (0) | 2025.01.17 |
| 백준 14501 : 퇴사 (0) | 2025.01.16 |




